Gamma correction on fragment shaders
This post is about the usage of gamma correction on fragment shaders, what it is and when it is appropriate to apply gamma correction. I am going to present the argument without any claim of completeness. Instead, I'll try to simplify the reasoning as much as possible, giving space to the math behind gamma correction. Please suggest improvements and corrections opening an issue on the website repository, thanks.
Input and output of a camera
Let $l$ be the luminance of a ray of light of a given colour. Do not worry about what a ray of light is, for the sake of simplicity, we say that $l$ is a positive number in $[0, 1]$.
When a camera detects the ray of light it produces a new positive number $F_{\gamma_c}(l)$ in interval $[0, 1]$. For the moment, just note that the function $F_{\gamma_c}$ depends on the parameter $\gamma_c$, a camera-specific positive number. Somehow, we may treat the camera as a black box that takes in input the colour luminance $l$ and returns on output the value $F_{\gamma_c}(l)$.
The final product of the camera elaboration is a digital image. Generally speaking, the digital image is defined by RGB values on each pixel. Each value on the red, green and blue channel is a value $F_{\gamma_c}(l)$ described above.
Input and output of a monitor
Digital images are visualized on monitors. In order to get back the original luminance value, monitors apply function $F^{-1}$ — which is the inverse of function $F$ — to return the value $F^{-1}_{\gamma_m}(F_{\gamma_c}(l))$ in $[0, 1]$. Note that the camera gamma and the monitor gamma may be not equal, only with $\gamma_c = \gamma_m$ we get back the original luminance value $l = F^{-1}_{\gamma}(F_{\gamma}(l))$. In other words, when $\gamma_{m}$ is not equal to $\gamma_{c}$ the image on the screen will have slightly different colours than the original colours captured by the camera. As with the camera, you may treat the monitor like a black box that takes in input the value $F_{\gamma_c}(l)$ stored on the digital image and returns the new positive value $F^{-1}_{\gamma_m}(F_{\gamma_c}(l))$.
The power-law expression
Summing up, cameras transform the original signal $l$ to $F_{\gamma_c}(l)$. Monitors, on the contrary, apply the inverse operation to get back the original signal on the screen. The diagram below represents the series of operation performed on the original luminance value. $$l \xrightarrow{\text{camera}} F_{\gamma_c}(l) \xrightarrow{\text{monitor}} F^{-1}_{\gamma_m}\Big(F_{\gamma_c}(l)\Big)$$
Function $F$ is the power-law expression $F_{\gamma}(l) = l^{\frac{1}{\gamma}}$. Function $F$ is monotonic in $[0,1]$, with $F_{\gamma}(0) = 0$ and $F_{\gamma}(1) = 1$. Most of the devices have a gamma in the interval around the value $2.2$. Taking $\gamma = 2.2$ we have $F_{\gamma}(0.5) \approx 0.73$, which means that the lower half of the domain is mapped to the $73\%$ of the codomain. In other words, the finite set of RGB colours privilege the encoding of lower luminance values over the higher ones.

Figure 1.
Diagram of the function $F_{\gamma}(l) = l^{1/\gamma}$. The blue rectangle highlights the fact that half of the domain is mapped to nearly three-quarters of the codomain. As a consequence of the non-linearity of the function, most of the available RGB space encodes low values of the luminance.
Gamma correction on fragment shaders
When working with fragment shaders, colour settings implicitly depend on the gamma inverse transformation operated by monitors. Artists adjust the RGB value $x$ in the shader according the colour $F^{-1}_{\gamma}(x) = x^{\gamma}$ visible on the screen. Note that the relationship between RGB values defined on the shader and the colours emitted on the screen is not linear.
We may avoid the implicit dependence on gamma — and the non-linear relationship between input and output — by adding a gamma correction to the colour $x$. This operation explicitly introduces a gamma parameter on the fragment shader. The gamma parameter on the shader may be tuned according to the gamma value of the output device. The formula to apply is the inverse of the gamma transformation operated by the monitor, i.e. the gamma correction $F(x) = x^{\frac{1}{\gamma}}$. Consequently, the emitted colour $(x^{\frac{1}{\gamma}})^{\gamma}$ is equal to the RGB colour $x$ defined on the shader.
The GLSL code in listing 1 produces two series of grey, both with RGB values between black and white. The first is linearly distributed in $[0, 1]$ and the second is gamma-corrected.
vec3 gammaCorrection (vec3 colour, float gamma) {
return pow(colour, vec3(1. / gamma));
}
vec4 gradientOfGrays (vec2 p) {
float N = 10.;
float c = floor(p.x * N) / (N - 1.);
vec3 colour = vec3(c, c, c);
return p.y > .5 ?
vec4(colour, 1.) :
vec4(gammaCorrection(colour, 2.2), 1.);
}Listing 1.
GLSL functions for the gamma correction and the visualisation of a gradient of greys. Usually, gamma correction happens at the very end of the fragment shader: gl_Fragcolour = vec4(gammaCorrection(colour, 2.2), 1.);.
Figure 2 is the resulting image. The gradient at the top shows the colours $x^{\gamma}$ obtained from the linearly distributed RGB values in $[0, 1]$. The gradient at the bottom shows the colours $(x^{1/\gamma})^{\gamma}$ obtained from the gamma-corrected RGB values.
At the bottom, despite the linear relationship between the RGB values and the emitted colours, we do not perceive a linear gradient. On the contrary, we perceive a linear gradient at the top of the image, where the emitted colours are $x^{\gamma}$.
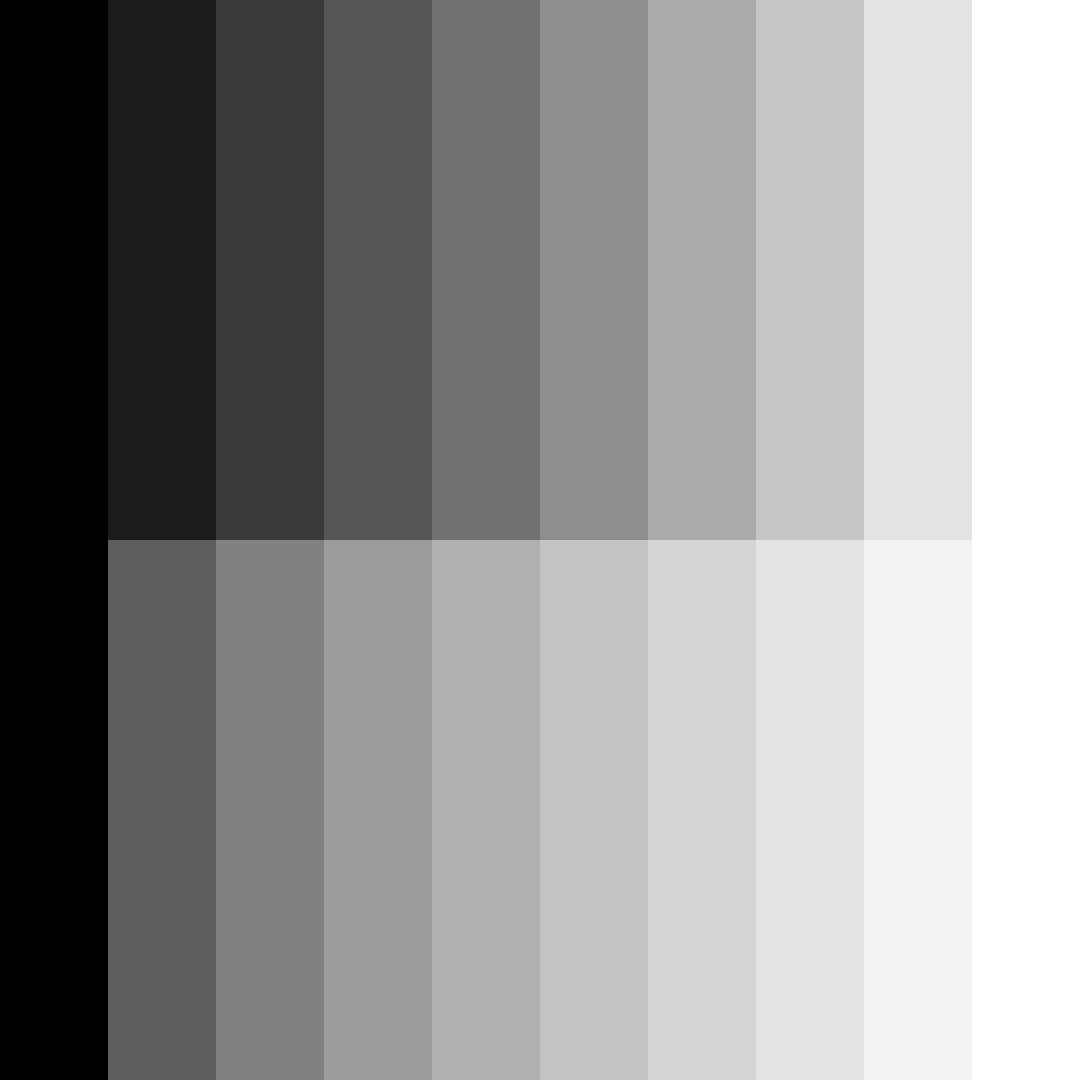
Figure 2.
Two gradients of greys, both going from black vec3(0.0, 0.0, 0.0) to white vec3(1.0, 1.0, 1.0). On the gradient at the top gamma correction is not applied, intermediate RGB values at position i are vec3(0.1, 0.1, 0.1) * i. Gamma correction is instead applied on the gradient at the bottom, intermediate RGB values at position i are pow(vec3(0.1, 0.1, 0.1) * i, 1./2.2). It is evident that, in spite of the linear distribution of luminance values at the bottom (i.e. the values emitted by the monitor), our perception of the resulting gradient of greys is not linear. At the top, on the contrary, where luminance values are not distributed linearly, we perceive a linear gradient.
Human colour perception
On the previous sections we described how cameras and monitors manage the luminance values, but we did not say why. Well, the reason is that human vision has a nonlinear perceptual response to luminance.
The perceptual response to luminance is called lightness and we, as humans, are more susceptible to changes between low luminance values than between high values. For this reason, cameras take advantage of the non-linear perception of light to optimize the usage of bits when encoding an image, privileging the encoding of lower luminance values over the higher ones. Let say, we apply to input luminance the same gamma-correction applied by cameras $F_{\gamma}(l) = l^{\frac{1}{\gamma}}$. Consequently, we perceive a linear gradient of greys from the series $x^{\gamma}$ described above. Please have a look at the GammaFAQ by Charles Poynton for more details.
The main purpose of gamma correction in video, desktop graphics, prepress, JPEG, and MPEG is to code light power into a perceptually-uniform domain, so as to obtain the best perceptual performance from a limited number of bits in each of the R, G, and B (or C, M, Y, and K) components.
Appropriate use of gamma correction
Do we need to apply gamma correction on fragment shaders? It depends on the meaning we assign to the RGB values we are setting on the shader. Look at the formula $F^{-1}_{\gamma_m}(F_{\gamma_c}(l)) = l$, it means that the monitor emits the same colour observed by the camera. Instead, the colours stored on the digital image are not equal to the original colours, they are gamma-corrected. When we are setting RGB colours on a shader, are they the original colours or the gamma-corrected? If we think they are the original colours, then we need to apply the gamma correction so to have the same colour on output: $(x^{\frac{1}{\gamma}})^{\gamma} = x$.
Do we need to treat the RGB values like the original colours? It becomes convenient if we are using mathematical formulas related to light, because calculations are easier. For example, let say $x$ and $y$ are the colours of two light beams, the colour of the sum of the beams is proportional to $x + y$. What if $x$ and $y$ are the implicitly gamma-corrected colours of the beams? Then the gamma-corrected colour of the sum of the beams would be proportional to $(x^{\gamma} + y^{\gamma})^{\frac{1}{\gamma}}$. Describing the light in a 3D scene with implicitly gamma-corrected colours is error-prone, for this reason the gamma correction is convenient. Gamma-correction becomes convenient when the rendering equation is involved, for example with volume ray casting.
